数据结构

Posted on Edited on In Valine:

数据结构总结

数据结构

什么是数据结构?

  • 数据元素:由数据项组成

  • 数据结构:
    • 数据之间的逻辑结构
    • 数据的存储结构

数据之间的逻辑结构

  • 集合结构(各个元素项之间没有关系)

  • 线性结构(排序问题)

    • 线性表

  • 非线性结构

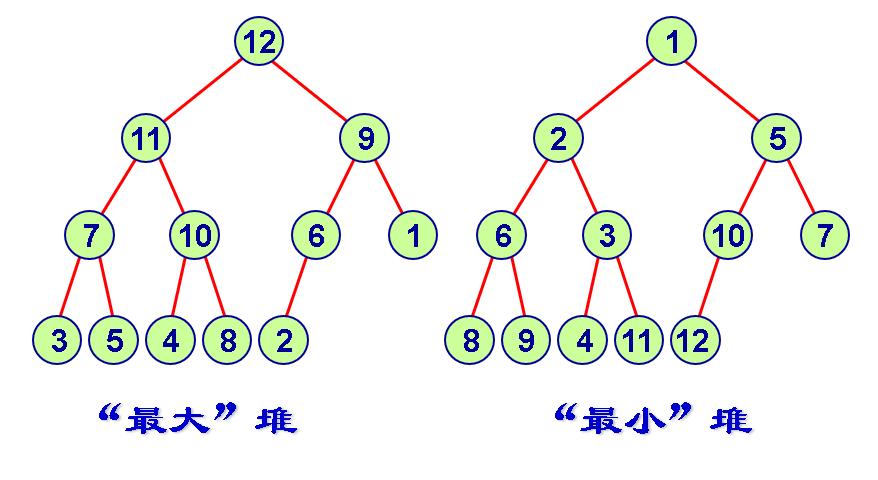
    • 树(传达命令,数据继承)

堆结构
堆结构
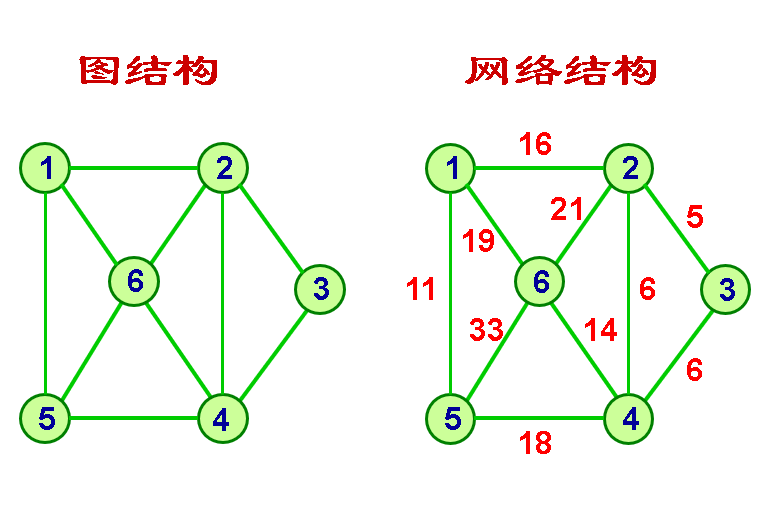
  • 图、网络(人际交往图,路由网络图)(网络:带权重的图)
图和网络
图和网络

数据元素的储存形式

  • 顺序存储

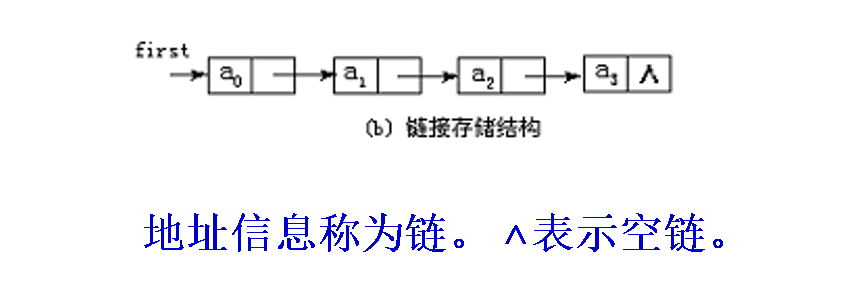
  • 链接存储

链接
链接

  • 索引存储

  • 散列存储

数据的运算

  • 创建
  • 清除:删除数据结构中的全部元素
  • 插入：在数据结构的指定位置上插入一个新元素；
  • 删除运算:将数据结构中的某个元素删除

算法

对特定问题的描述步骤，有穷的指令集合

程序=数据结构+算法

特点：

  • 输入:\(\ge0\)
  • 输出：\(\ge 1\)
  • 确定性：没有二义性
  • 可执行性(大象塞进冰箱没有可执行性)
  • 有穷性

算法的时间复杂度和空间复杂度

程序步

image-20220316231442955
image-20220316231442955

时间复杂度，大\(O\)标记法，常见的时间复杂度

线性表

定义:除了头结点和尾节点之外,其他结点有且仅有一个前驱和一个后继称为线性表

顺序表(顺序存取)

实现方式:数组

主要注意操作:

删除操作\(O(n)\)

删除操作是删除表的第i (\(1\le i\le n+1\))个位置的数据主要实现方式如下(需要将后面的位置向前移动):

1
2
3
4
5
for(int j=i;j<length;j++)
{
    //从第i个位置开始,所有数据向前移动
    data[j-1]=data[j];
}

插入操作\(O(n)\)

插入操作是在表的第i (\(1\le i\le n+1\))个位置插入一个新元素\(x\),主要实现方式如下:

1
2
3
4
5
6
7
for(int j=length;j>=i;j--)
{
    data[j]=data[j-1];
}
//下标为i-1的元素的位置为i-1
data[i-1]=x;
length++;

缺点:

  • 插入和删除的复杂度太高,都达到了\(O(n)\)
  • 容量不好确定
  • 必须要连续的存储空间

链式存储(顺序存取)

单链表(带头结点)

  1. 插入操作(p结点之后)(\(O(n)\))

    说明:时间复杂度尾\(O(n)\),主要花在了找查的上面,实际时间只需\(O(1)\).

1
2
3
4
5
Node * insert= new Node;
insert->data = x;
//p->next一定要先传出去
insert->next = p->next;
p->next = insert;

  1. 删除操作(p结点之后)(\(O(n)\))

    说明:时间复杂度尾\(O(n)\),主要花在了找查的上面,实际时间只需\(O(1)\).

1
2
3
4
Node * q = p->next;
//要删除的结点的下一个位置一定要先传出去
p->next = q->next;
delete q;
  1. 初始化带头结点的单链表
1
2
first = new Node<DateType>;
fisrt->next = null;
  1. 两种插入新元素的方式

  • 头插法(\(O(1)\))

  • 尾插法(\(O(n)\))

    说明:时间复杂度尾\(O(n)\),主要花在了找查的上面,实际时间只需\(O(1)\).

1
2
3
4
5
6
7
p = first ;
while (p->next!=Null)
{
    p= p->next;
}
s->data = x;
p->next =s;

双链表

  1. 插入操作(在结点p后面插入一个新结点s)
1
2
3
4
5
s->prior = p;
//这一步一定要在p->next 改变之前
s->next = p->next;
p->next->prior= s;
p->next = s;
  1. 删除操作(删除p结点)
1
2
3
4
//这个地方没有前后顺序
p->prior->next = p->next;
p->next->prior =  p->prior;
delete p;

循环链表

循环链表一般使用尾指针rear,在循环链表的遍历中,为了判断其是否遍历完成,所以可以用p==rear来判断

两种储存方式的比较

顺序表:

  • 查找:\(O(1)\)
  • 插入:\(O(n)\)
  • 删除:\(O(n)\)

链表:

  • 查找:\(O(n)\)
  • 插入:\(O(1)\)
  • 删除:\(O(n)\)

线性表应用

静态链表

约瑟夫环

问题描述:

0,1,···,n-1这n个数字排成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字（删除后从下一个数字开始计数）。求出这个圆圈里剩下的最后一个数字。

例如，0、1、2、3、4这5个数字组成一个圆圈，从数字0开始每次删除第3个数字，则删除的前4个数字依次是2、0、4、1，因此最后剩下的数字是3。

抽象数据类型:

构造函数:环的长度n和密码m

  1. 第一步:构造一个长度为n的约瑟夫环

  2. 第二步:使用密码m进行求解约瑟夫环的答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//使用密码求解环的答案
int Josph(int m)
{
    //从第一个元素开始
    Node *pre = rear;Node *p = rear->next;
    //直到只剩下一个元素的时候跳出循环
    while(p!=pre)
    {
        //循环遍历直到p走过m步,因为约瑟夫环要包括自己
        //所以只能走m-1
        for(int i=0;i<m-1;i++)
        {
            p=p->next;
            pre=p->next;
        }
        pre->next=p->next;
        delete p;
        p=pre->next;
    }
}

一元多项式求和

问题:多项式\(A(x)=a_0+a_1x+a_2x^2+..a_nx^n\)和\(B(x)=b_0+b_1x+b_2x^2+..b_nx^n\)合并

分析:合并的时候,有一些项数是都存在,有一些项数只是A或者B存在,那么,这种情况下我们要假设A,B都已经按照从小到大的幂次排列好,这时,我们只需要将一项一项进行比较,观察他们是否相等,相等则合并,不相等则不合并

抽象数据类型:

元素:长度足够的数组data 每一项:系数xishu,幂次mici

操作:合并A,B,运算符重载

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
void add(Poly B)
{
    //设置一个头结点,所以i从1开始
    int i=1;int j=1;
    int i_=0;
   
    //只有当两者都没有达到最后一个元素的时候,不能停止
    //如果是链表的话应该是判断指针是否为空
    while(i!=length+1&&j=!length+1)
    {
        //如果幂次相等,则系数相加
       	if(this->data[i].mici==B->data[j].mici)
        {
            //当系数的和不为0的时候,相加
            if(this->data[i].xishu+B->data[j].xishu!=0)
            {
                this->data[i].xishu=this->data[i].xishu+B->data[j].xishu;
                i++;j++;i_++;
            }
            //如果系数和为0,则将这个节点删除,i不需要自加
            else{
                Delete(this->data[i]);
                j++
            }
        }
        
        
        //如果A的第i位置的幂次大于B的第j个位置
        //那么B的这个节点应该放在A的前面一个位置
        if(this->data[i].mici>B->data[j].mici)
        {
            //将B的j节点插入i的前面一个位置
            //保持i_始终在i的前面一个位置
            Insert(B->data[j],i_);
            j++;i_++;
        }
        
        //A的第i位置小于B的第j个位置
        //说明A要往后走一个位置再比较
        if(this->data[i].mici<B->data[j].mici)
        {
            i++;i_++;
        }
    }
    
}

栈和队列

栈结构(Stack)

  1. 顺序栈(数组实现)

    栈空判断:top==-1

    栈的长度StackSize

  2. 链栈

    单链表的表头为栈顶(头插法)

问题:当进入栈的顺序为1,2,3,4,5...n时,请问可能出栈的序列有多少种?

结果:\(\frac{1}{n+1}C_{2n}^{n}\)

元素个数变化较大的时候用链栈,否则用顺序栈

队列

循环队列(数组实现)

  1. 顺序队列的存储结构(数组),入队出队时间复杂化度为\(O(1)\),空间利用率为n-1

  2. 解决假溢出:rear=(rear+1)%QueueSize

  3. 循环队列判断是否满的判断:(rear+1)%QueueSize=front

链队列

  1. 队头:头指针,时间复杂度为\(O(1)\)
  2. 入队:尾插法
  3. 出队,头出发(不要删除头结点)
1
2
3
4
5
6
7
8
9
10
11
//出队代码
p=first->next;
first->next=p->next;
//删除结点的时候一定要记得保存
int x= p->data;
//注意尾结点,不要让其指向空
if(first->next==NULL)
{
    rear=first;
}
return x;

应用举例

  1. 两栈共享空间

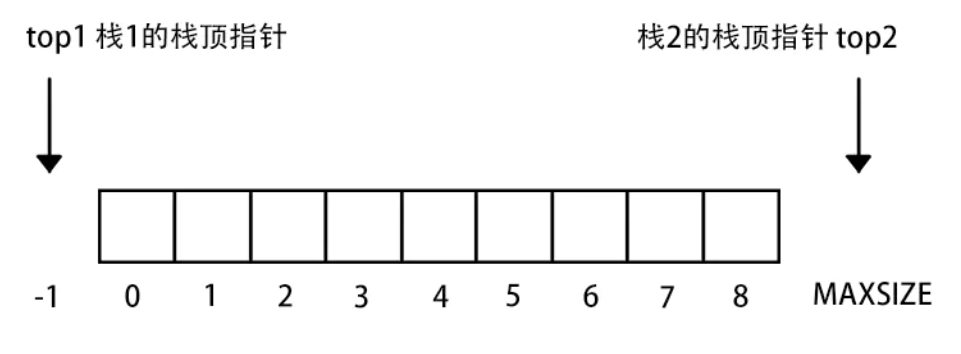
image-20220430231223168

括号匹配问题

使用栈来匹配括号,查看代码是否是多了括号或者少了括号

算法:Match(str)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
top = -1;
for(int i=0;str[i]!='\0';i++)
{
    //如果判断为左括号,进栈
    if(str[i]=='(')
    {
        top++;
    }
    //判断为右括号,出栈
    else if(str[i]==')')
    {
        top--;
    }
}
if(top!=-1)
{
    //如果栈中有括号或者使用了更多的括号,返回-1
    return -1;
}
else
{
    return 0;
}

表达式求值

设运算符有+,-,*,/,#,其中#号是界定符,求出给的表达式的结果:假设给的表达式为 \[ 3\times 3+(6/5+7)*4-9 \]

​ 一个表达式的输出一共有两种情况,一种是数字,一种是符号,我们假设有两个栈,一个是符号栈,一个是数据栈,首先要判断进来的这个是不是一个符号,其次他的优先级是否高于现在栈中栈顶元素的符号,如果高于,那么这个时候我们让它进栈,如果不高于,那么,我们让栈中栈顶元素出栈,,对数据进行运算,直到其优先级小于入栈符号的优先级,然后新的符号压入栈中.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
SymbolStack.push('#')
for(int i=0;!SymbolStack.isempty();i++)
{
    str=str_[i];
    //进入栈之后判断一下它是否是符号
    //是不是优先级较高的
    while(IssSymbol(str)&&!IsPriority(str))
    {
        a=NumberStack.pop();
        b=NumberStack.pop();
        NumberStack.push(Calculate(b,a));
    }
    //如果是符号,而且优先级高,则入栈
    if(IssSymbol(str)&&IsPriority(str))
    {
        SymbolStack.push(str);
    }
    //如果是数字,则让其进入数字栈
    else
    {
        NumberStack.push(str.toInt());
    }
    
}

递归

递归的主要组成部分

  • 基础情况
  • 递归部分

汉诺塔求解

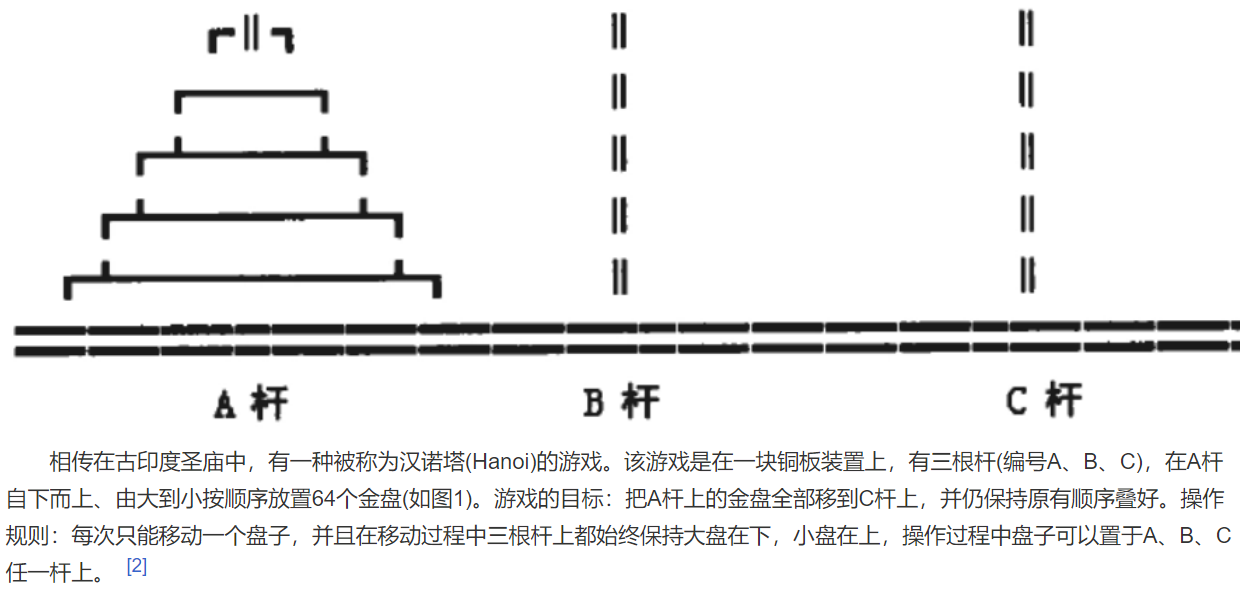
image-20220501195358429

解决方法:

:one: 首先假设样本数量比较小,例如只有一个盘子的时候,那么我们需要做的是:A--->C

如果是两个盘子:第一步:将上面的盘子移到B,将A的盘子移到C,再把B上面的移动到C:A--->B,A--->c,B--->c

如果是三个盘子:第一步,想办法把A上面2个盘子移到到B,再把A上的移动到C,最后想办法把B上的移动到C:A(2)--->B,A--->C,B(2)--->C

:two:现在考虑更加朴实的情况:n个盘子:则算法的思路为:A(n-1)--->B,A--->C,B--->C

:three: 好!现在算上想清楚了,基础条件:n=1:直接移动,如果n!=1的时候,就借助B,再移动到C

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//Move函数:A通过借助B移动到C
Move(A,B,C,n)
{
    if(n==1)
    {
        cout<<A<<'--->'<<C;
    }
    else
    {
        //将A上面的n-1个盘子通过A移动到B
		Move(A,C,B,n-1);
        
        //将A的最底下的盘子一次移到C
        Move(A,B,C,1);
        
        //将B上所有的盘子想方法移动到C
        Move(B,A,C,n-1);
    }
}

N皇后问题