出租车载客模型
数学建模.Are you kidding me ? 😭我要疯了!
问题分析
- 司机去等候区等候,需要一定的时间,等待时间取决于出租车和乘客数量
- 不载客人出机场,直接去市区把客人拉回来,但是空载费用和潜在用户的损失
- 已知:蓄车池车的数量,司机个人的判断(决策),航班的数量,人数
问题一
分析影响司机决策的因素,其与乘客数量,不同情况的收益,选出最优决策
因素确定:
时间\(T_0\in[T_1,T_2]\)航班总数\(N_{f2}\),人数为\(M_{p2}\).
出租车总数,等待时间不超过预期\(N_{taxi}\),选择等待
空载率\(\beta\)和机场通行率,空载率越低,载客的可能性越高,更倾向于半路接客,通行能力为\(v_{leave}\),是指单位时间内通过出租车载客离开的组数
机场与市中心的距离\(L\),距离越大越倾向等待,时间的等待上线提高
航班载客数: \[ U(M_1,M_2)=\begin{cases}0&M_0\notin[M_1.M_2]\\\frac{1}{M_2-M_1}&M_0\in[M_1,M_2]\end{cases} \]
\[ M_p=M_{p1}+M_{p2}\\ M_{p1}=\sum_{i=1}^{N_{f1}}M_{0i},M_{p2}=\sum_{i=1}^{N_{f2}}M_{0i} \]
\(N_{f1}\)为为时间\([T_1,T_0]\)内机场的预计滞留人数,\(N_{f2}\)为时间\([T_0,T_2]\)内机场来的人数
其中\(M_{p1}\)为司机估计的机场滞留人数,\(M_{p2}\)为司机估计机场抵达人数
里程:假设里程正态分布 \[ \xi(x)\sim N(\mu,\sigma^2) \] 概率密度图为

收入
计价规则: \[ \begin{cases}p_0&x\le a\\p_0+p_1(x-a)&a<x\le b \\p_0+p_1(b-a)+p_2(x-b)&x>b\end{cases} \] 时间成本:
空载: \(C_{free}\)
等待:\(C_{wait}\)
等待时间成本\(M_{plain}\)为时间段内机场乘客选择乘坐出租车的总数,与机场的总乘客数\(M_p\)成比例关系,即\(M_{plain}=\mu_1M_p\),\(\mu_1\)为机场乘客选择出租车的比例。 \[ t_{wait}=\frac{M_{plain}}{v_{leave}} \] 总出行人数除以单位时间出行人数
出租行驶载客:概率\(\gamma=1-\beta\).司机载客时间为\(L_{pa}=L_{drive}\cdot\gamma\),其中时间成本的具体表达式为: \[ C_{time}=C_{wait}+C_{free}=G(L_{paw})+G(L_{paf})\\L_{paw}=t_{wait}\cdot v_{taix} \cdot \gamma;L_{paf}=t_{free}\cdot v_{taix}\cdot \gamma \] \(G(L_{paw}),G(L_{paf})\)为等待和空载的计价收入
成本
\[ C_g(x)=A \cdot S_{gax}\cdot x \]
方案确立
等待 \[ W_1=G(x)-C_g(x)-C_{time}\\ =G(x)-C_{g}(L)-G\left(t_{\text {wait }} v_{\text {taxi }} \gamma\right)-G\left(t_{\text {free }} v_{\text {taxi }} \gamma\right)\\ t_{\text {free }}=\frac{L-x}{v_{\text {taxi }}} \]
空载时间为总路程减去载客路程除以汽车的速度,
空载 \[ W_2=-C_g(x)-C_{time}=-C_g(L)-G(t_{free}v_{taxi}\gamma)\\ t_{free}=\frac{L}{v_{taxi}} \]
模型求解

假设参数,\(L=25.1km\).出租车的空载率为\(\beta=0.4\),车速为\(v_{leave}=1\)。出租车出行占总人数比例为\(\mu_1=0.3\),平均同行人数为\(\mu_2=2\),后期设置一般数据验证
问题二
选一个机场,给出司机的选择(司机的决策(数据))说出合理性和因素的依赖性
数据收集
北京首都机场
表格数据
类型 9~10 10~11 11~12 忙季(节假日) 30 27 15 淡季(工作日) 1 3 3 价格 \[ 晚上:G(x)\left\{\begin{array}{lc} 13, & x \leq 3 \\ 13+2.76 \times(x-3), & 3<x \leq 15 \\ 13+2.76 \times 12+2.76 \times 1.5 \times(x-15), & x>15 \end{array}\right. \]
\[ 早上:G(x)=\left\{\begin{array}{lc} 13, & x \leq 3 \\ 13+2.76 \times(x-3), & 3<x \leq 15 \\ 13+2.76 \times 12+2.76 \times 1.5 \times(x-15), & x>15 \end{array}\right. \]
代入数据,可以得到闲暇时期和忙碌时期的不同图像

然后可以根据排队方案一的收益

image-20210815164119981 不同距离和行驶的速度也因为时间成本是不一样的得到的收益

问题三
有两条道路,如何安排让乘客和司机的等待时间最小
建立模型:
目标函数:乘车效率
决策变量:上车点数
环境参量:单位时间,达到机场的平均出租车数和平均人数为\(\alpha_1\),\(\lambda_1\)为到达机场的人数,\(\lambda_2\)平均每分钟到达机场的乘客数,\(\alpha_1=\frac{\lambda_1}{\lambda_2}\);
模型:
\[\begin{aligned}max \quad\eta=\frac{1}{\sum_{i=1}^{n}\frac{t_{pi}}{n}+\sum_{j=1}^{m}\frac{t_{cj}}{m}}\\s.t.\quad k\le12\end{aligned}\]
求解
问题四
收益和里程成正比,对于短途的载客给予优先权,使得大家的工资尽量均衡,该如何给其优先权,注意这里假设的长途和短途的定义
短途
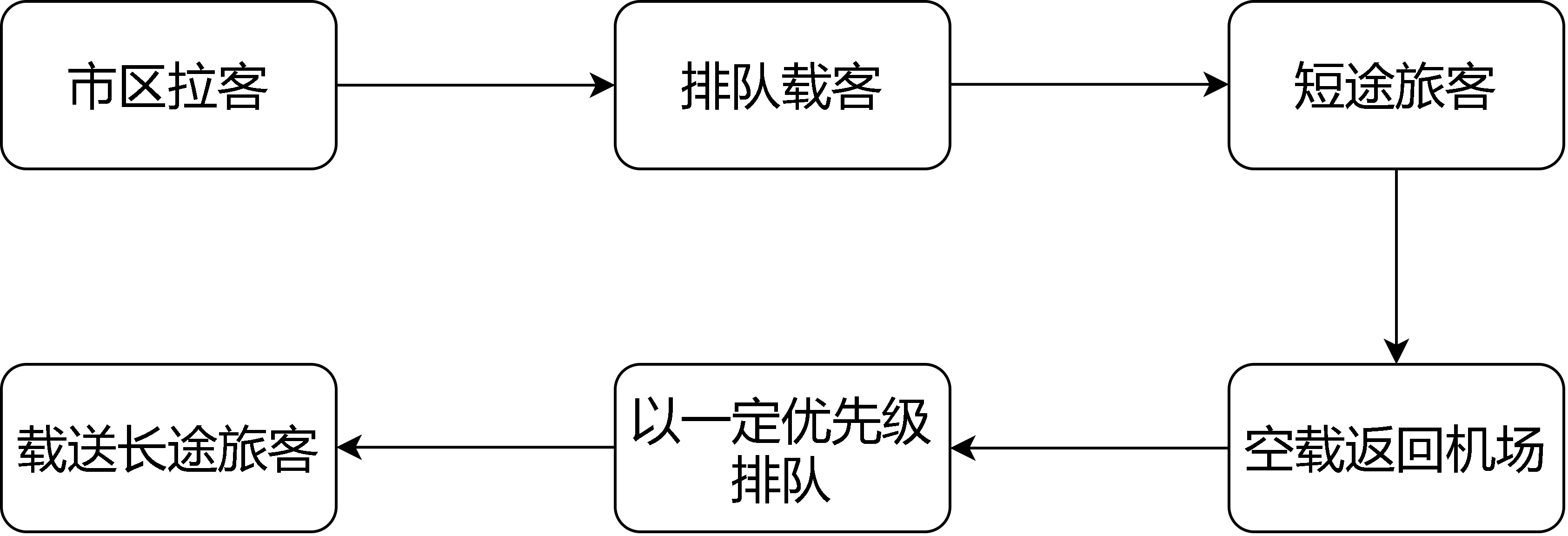
\[ \begin{aligned} &\beta_{\text {short }}=\frac{m / v_{\text {leave }}+x_{\text {share }} / v_{\text {tax } i}+m_{0} / v_{\text {leave }}}{L / v_{\text {taxi }}+m / v_{\text {leave }}+x_{\text {short }} / v_{\text {taxi }}+x_{\text {short }} / v_{\text {taxi }}+m_{0} / v_{\text {leave }}+L / v_{\text {taxi }}} \\ &\qquad=\frac{m / v_{\text {leave }}+x_{\text {short }} / v_{\text {taxi }}+m_{0} / v_{\text {leave }}}{2 L / v_{\text {taxi }}+m / v_{\text {leave }}+2 x_{\text {taxi }} / v_{\text {taxi }}+m_{0} / v_{\text {leave }}} \\& W_{\text {short }}=\frac{2 W_{L}+W_{x}}{2 L / v_{\text {taxi }}+m / v_{\text {leave }}+2 x_{\text {short }} / v_{\text {taxt }}+m_{0} / v_{\text {leave }}} \end{aligned} \]
长途

\[ \beta_{long}=\frac{m/v_{leave}}{2L/v_{taxi}+m/v_{leave}}\qquad W_{long}=\frac{2W_L+W_{city}(T)}{2L/v_{taxi}+m/v_{leave}+T} \]
- \(\epsilon_1\)和\(\epsilon_2\)为权重因子,\(\Delta\beta_{max}\)和\(\Delta W_{max}\)为归一化因子,变量计算方法如下: \[ \begin{aligned}\min \quad g\left(m_{0}\right)=\varepsilon_{1}\left(\frac{\beta_{\text {l0ng }}-\beta_{\text {short }}}{\Delta \beta_{\max }}\right)^{2}+\varepsilon_{2}\left(\frac{W_{\text {long }}-W_{\text {short }}}{\Delta W_{\max }}\right)^{2}\\\begin{cases} \beta_{\text {short }}=\frac{m / v_{\text {leave }}+x / v_{\text {taxi }}+m_{0} / v_{\text {leave }}}{2 L / v_{\text {taxi }}+m / v_{\text {leave }}+2 x / v_{\text {taxi }}+m_{0} / v_{\text {leave }}} \\ W_{\text {short }}=\frac{2 W_{L}+W_{x}}{2 L / v_{\text {taxi }}+m / v_{\text {leave }}+2 x / v_{\text {taxi }}+m_{0} / v_{\text {leave }}} \\ \beta_{\text {long }}=\frac{m / v_{\text {leave }}}{2 L / v_{\text {taxi }}+m / v_{\text {leave }}} \\ W_{\text {long }}=\frac{2 W_{L}+W_{\text {city }}(T)}{2 L / v_{\text {taxi }}+m / v_{\text {leave }}+T} \end{cases}\end{aligned} \]
计算即可