动态规划入门

Posted on Edited on In Valine:

​ 之前没搞懂的动态规划，现在强行试了一下，欢迎大家指导！

Fibonacci Sequence

  • 递归的思想
    • 要求第n项，先求n-1和n-2项，若n-1和n-2项为1,2则都令为1
    • Fobonacci Sequence复杂度比较高，不适合大数据计算，例如当n=100时，计算起来就十分的慢
1
2
3
4
5
def  fibo(n):
    if n==1 or n==2:
        return 1
    else:
        return fibo(n-1)+fibo(n-2)

​ 既然Fibonacci数列的递归计算如此复杂，那么，我们应该想什么办法来优化整个算法呢，我们考虑到，Fibonacci之所以复杂，是因为递归的存在，导致整个程序的时间复杂度都十分的高那么我们有没有简单一点的方法呢,对了，我们可以采用记录的方式，将每一个点之前的Fibonacci的数值都保存下来

1
2
3
4
5
6
7
8
9
10
def Fibo(n):
    memo=[1]*n     #新建一个备忘录，记录每一个点的斐波拉切数列值，初始为[1,1,1,1....]
    for i in range(n):
        if i<=1:
            memo[i]=1   #给备忘录的第一个元素和第二个元素附一个1的初值
        else:
            memo[i]=memo[i-1]+memo[i-2] #生成整个memo数组
    return memo[i]   #返回memo最后一个值，就是整个要求的的最大值
#调用一下
Fibo(100)

​ 我们调用了相关的带有memo的Fibo函数之后，明显发现，整个速度提升了很多，整个计算没有超过一秒钟，显然，这种方法是很有效的，我们称这个memo为DP数组

House-robber

  • 你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。
  • 输入：[1,2,3,1]

输出：4

解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。

偷窃到的最高金额 = 1 + 3 = 4 。

对于小偷问题，我们可以这么去思考，就是我们新建一个DP数组，用来储存小偷走到这个点时之前可以得到的最大的收益，如果按照这种思路，然后去整个数组的最大值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def steal():
    nums=[1,2,3,1]   #每个房子有的金额（金额数组）
    memo=[1]*len(nums)    #新建一个DP数组，这个数组就是记录到那个点的最大值
    for i in  range(len(memo)):     #完善数组，for循环，开始从第一个位置开始填充数组
        if i==0:
            memo[i]=nums[i]         #前两家偷的时候，只能偷其中一家，所以最大值为两家中的一家
        elif i==1:
            memo[i]=max(nums[i],nums[i-1])     #第二家的最大金额，应该是偷第一家和偷第二家的最大之一
        else:
            memo[i]=max(memo[i-2]+nums[i],memo[i-1])    #用户大于第三家之后，数组的值应该为偷这一家(不能连续偷)(memo[i-2]+nums[i])
            #如果偷了的金额没有不偷多，那就不偷
    print(max(memo))
    print(memo)  
steal()

Maximum value of gifts

在一个 m*n 的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于 0）。你可以从棋盘的左上角开始拿格子里的礼物，并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值，请计算你最多能拿到多少价值的礼物？

输入:

[

[1,3,1],

[1,5,1],

[4,2,1]

]

输出: 12

解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物

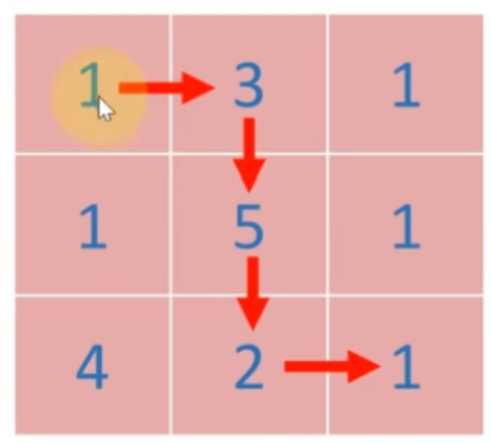
image-20210819174221935

​ 我们要计算从左上角到右下角最大的礼物价值，我们不妨这么思考，我们还是新建一个DP数组，这个DP数组应该是二维的，然后考虑DP数组是左上角到达每个点的最大价值，又因为路线只能右走或者下走。所以当其为横向、纵向的边界时，我们只要考虑左边、上面

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def gift():
    a=[
      [1,3,1],
      [1,5,1],
      [4,2,1]
    ]
    r,c=len(a),len(a[0])   #读取出数组的长度r代表row，c代表column
    memo=[]
    for i in range(r):
        memo.append([1]*c)   #初始化DP数组，让DP数组的大小为原来a的大小
    for i in range(r):       #遍历整个二维的a，然后开始填充memo的每一个地方
        for j in range(c):
            if i==0 and j==0:
                memo[i][j]=a[i][j]    #第一个位置为起点，所以必须为a的第一个值
            elif i==0:
                memo[i][j]=memo[i][j-1]+a[i][j]    #当i=0时，说明第一行数据，由于只能右走和下走，所以
                                                    #这里是右走
            elif j==0:
                memo[i][j]=memo[i-1][j]+a[i][j]    #当i=0时，说明第一列数据，由于只能右走和下走，所以
                                                    #这里是下走
            else:
                memo[i][j]=max(memo[i][j-1]+a[i][j],memo[i-1][j]+a[i][j])
                                                #当i!=0,j!=0时，可以右走和下走
                
    print(memo)

Coins exchange

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。你可以认为每种硬币的数量是无限的。

输入：coins = [1, 2, 5], S = 11

输出：3

解释：11 = 5 + 5 + 1

输入：coins = [2], S = 3

输出：-1

image-20210819174503970

\[ f(x)=min\{f(x-c_1),f(x-c_2),...f(x-c_m)\}+1 \]

如果\(x-c_i<0\)，则令\(f(x-c_i)=\infty\)这样就不会选这个\(f(x-c_i)\)了

如果\(x-c_i=0\),那么\(f(x-c_i)=0\)即\(f(0)=0\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def change_coins():
    coins,S=[1,2,5],11    #拥有的硬币的种类，个数
    dp={}                 #定义一个dp的字典，记录到每一元钱，所需要的硬币个数
    temp=[]
    for i  in range(S+1):   #一直需要到11，所以这里是0-12
        for j in coins:
            if i-j==0:     #先判断这个x-c_i是不是等于0，如果是，令min{....}的数组中添加0
                temp.append(0)
            elif i-j<0:    #在判断i-j是不是小于0，如果是，这说明这条路不行，于是令min{...}的...中添加一个数1000
                temp.append(1000) 
            else:          #在其他的情况下都是满足的，那么可以按照上面的公式，在这个可能的结果中添加一个数为dp.get(i-j)
                temp.append(dp.get(i-j))
        dp[i]=min(temp)+1  #dp[i]则应该为上面的一个数组中的一个数的最小值加一即min{[....]}+1
        temp=[]            #记得给数组归0
#     print(dp)
    return dp
change_coins()

现在我们已经知道硬币的最少组合为3，那我们如何得到是哪些硬币的组合

思路： 我们可以将S=11的最小硬币数是3分解一下，例如，硬币数是3，说明[1,2,5]中的三个可以组成，于是我们可以一个一个的遍历，看当11减去其中的一些数之后判断一下剩余的需要的最小硬币数是不是2，例如:11-1,然后:凑成10元的所需硬币数最小是2吗，是的话，跳出遍历，选择这一10继续分解，不是的话，继续遍历下面的，直到S=0说明已经遍历到0了，可以结束

如何得到硬币的组合呢（5，5，1）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def find_coins(S):
    dp=change_coins()    #调用上面的硬币交换得到dp数组
    coins=[1,2,5]       #硬币的种类为1,2,5
    n=dp.get(S)         #第一步先调出S的最小硬币数
    dp[0]=0             #给dp数组的0元素归0
    go,coin_cate=[],[]   #go数组可以记录整个换钱的过程，coin_cate可以看出每个过程所使用的硬币的金额
    while dp.get(S,0)-1>=0:     #当dp.get(S,0)-1=0时，说明S为非零且属于[1,2,5]
        for i in coins:         #从[1,2,5]中一个个取数
            if n-1==dp.get(S-i):    #如果有需要凑成S-i的钱的最小个数与S需要的最小个数只相差1，那么符合
                                    #取其中一种情况即可
                go.append(S-i)      #把这个可以凑成的金额添加到路径里
                coin_cate.append(i)  #把这次使用的种类添加到硬币的种类里
                S=S-i                #给S从新赋值，让S=S-i，以便寻找下一轮循环
                break                #只要找到满足条件的一个coins即可，不需要全部找到
        n=dp.get(S,0)
        if S==0:                     #如果S=0，说明整个分解可凑的钱程序已经已经走到需要凑0元的情况，
                                    #显然这种情况可以直接结束程序
            break
    print(go,coin_cate)
find_coins(11)

Knapsack Problem

​ 有10件货物要从甲地运送到乙地，每件货物的重量(单位:吨)和利润(单位:元)

如下表所示:

image-20210819174323036

​ 由于只有--辆最大载重为30t的货车能用来运送货物，所以只能选择部分货物配送，要求确定运送哪些货物，使得运送这些货物的总利润最大。

思路：

​ 有m件物品，第i件物品的利润为\(v_i\)重量为\(w_i\)背包的总重量为W.

原问题:在满足重量约束的条件下，将这m个物品选择性放入容量为W的背包所能获得的最大利润

子问题:在满足重量的约束条件下，将i(\(i\le m\))件物品选择性放入容量为j(\(j \le W\))的背包所获得的最大利润 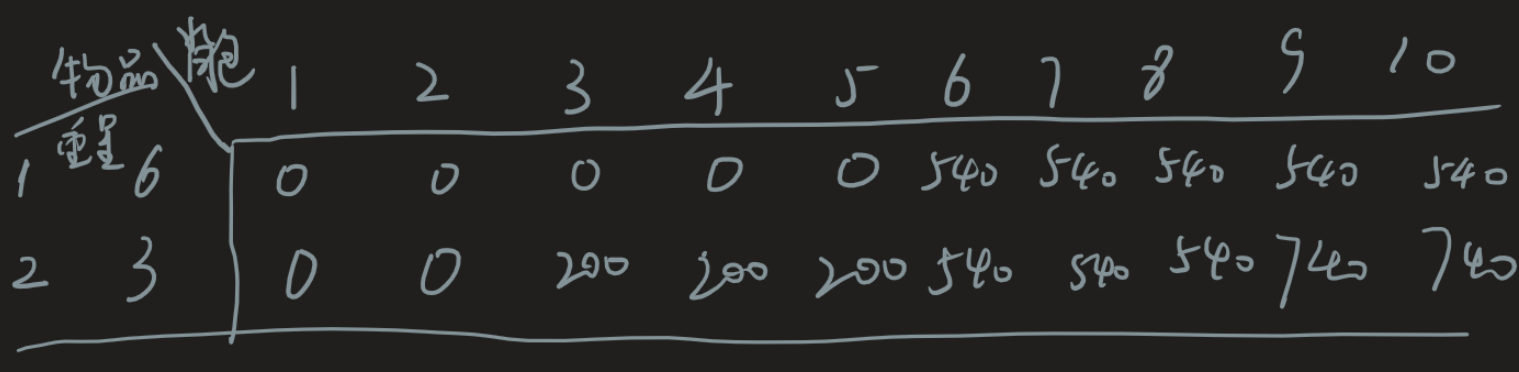image-20210819174526184

状态分析:

​ 我们要讲m件商品装进容量为W的背包，我们可以假设背包是从1,2,3,4...增大的容量，物品从第一次只装第一个产品，然后慢慢推广到前i个产品，所以DP表格其实是在背包容量为i的情况下，能装的礼物的最大价值

​ 对于第一行来说，装的物品为第一个物品，所以只需要判断背包容量是否大于第一件物品的重量，若大于，则最大价值为第一件物品的价值

​ 对于第一列来说，背包容量为1，装进前i件物品的最大价值，由于物品的重量始终为整数，所以在前i件物品里，我们要看有没有总量为1的物品，若没有，则什么也装不进去，那么最大价值为0，若有(可能有几个)，则去前i个产品中重量为1的所有物品中价值最大的那个为该点dp表的值

​ 对于其它的列来说，需要用到状态转移方程，对于要求前\(i\)件物品装进容量为\(j\)的背包，在\(i-1\)的基础上只需要考虑到底装不装第\(i\)件物品，那么怎么考虑呢？要装第\(i\)件物品首先，第\(i\)件物品的重量必须小于背包的容量所以有: ​ \(j-weight(i)>=0\)才去判断: \[ max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]) \]

它的意思是如果第i件物品装的下，那么就去判断不装这件物品和在没装这件物品，也就是dp[i-1][j-weight[i]]的最大价值，然后加上这件物品的价值。这样就可推出整个dp数组，而数组的最后一个元素，就是我们要求的最大价值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
items=[(1,6,540),(2,3,200),(3,4,180),(4,5,350),(5,1,60),(6,2,150),(7,3,280),(8,5,450),(9,4,320),(10,2,120)]
# 定义一个含有所有的价值的数组
weight=30   # 定义背包的重量
def bag_problem():
    dp=[]     #定义dp数组
    for i in range(len(items)):    #初始化dp数组
        dp.append([0]*weight)
    for i in range(len(items)):      #双重遍历开始填充数组
        for j in range(weight):
            if i==0 :
                if j>=items[0][1]-1:    #背包大小大于等于物体的大小，物体大小为定值，则为items的价值
                    dp[i][j]=items[0][2]
                else :
                    dp[i][j]=0          #如果背包太小，那就价值为0
            if j==0 :                   #探究第一列的值
                if items[i][1]==1:
                    dp[i][j]=max(dp[i-1][0],items[i][2])      #如果可以装进去，前i个产品中重量为1的所有物品中价值最大
                else:
                    dp[i][j]=dp[i-1][j]             #重量超过一的物品无法装入，直接用重量为1的物体价值最大的那个作为dp[i][j]
            else:                      #探究其它列
#                 print(j)
                if j+1-items[i][1]<0:   #如果背包转不下就只能是dp[i-1][j],相当于不装第i件
                    dp[i][j]=dp[i-1][j]
                else:                   #其它情况判断背包产生的价值是否大于没装时候产生的价值
                    dp[i][j]=max(dp[i-1][j],dp[i-1][j-items[i][1]]+items[i][2])
    return dp
#     for c in dp:
#         print(c)
for i in bag_problem():
    print(i)